Tree Infection

So what's the shortest amount of time a tree can be "infected"?

题面翻译

题意描述

一个树是一个无环连通图。一个有根树有一个被称作“根结点”的结点。对于任意一个非根结点 $v$ ，其父结点是从根结点到结点 $v$ 最短路径上的前一个结点。结点 $v$ 的子结点包括所有以 $v$ 为父结点 的结点。

给定一个有 $n$ 个结点的有根树。结点 $1$ 即为根结点。一开始，该树上所有结点均是“健康”的。

每一秒你会进行两次操作——先是传播操作，然后是注射操作，定义如下。

• 传播操作：对于每个结点 $v$ ，若该结点至少有一个子结点被“感染”，则你可以“感染”顶点 $v$ 任意一个其他的子结点。
• 注射：你可以选择任意一个“健康”的结点并使它变为“感染”状态。

这程每秒会重复一次知道整个树的结点都处于“感染”状态。你需要找到使整个树被“感染”的最短时间（秒数）。

输入格式

有多个测试数据。第一行输入整数 $t$ ，代表有 $t$ 组数据。每组数据格式如下。

第一行给定整数 $n$ ，表示整个树共有 $n$ 个结点。

第二行输入 $n-1$ 个整数 $p_{2...i-1}$ ，第 $p_i$ 个整数表示 $i$ 号结点的父节点是 $p_i$ 号结点。

输出格式

共 $t$ 行，每行一个整数，即使整个树被“感染”的最短时间（秒数）。

数据范围

• $1 \le t \le 10^4$
• $2 \le n \le 2 \times 10^5$
• $1 \le p_i \le n$
• $\sum \limits_{i=1} ^t n_i \le 2 \times 10^5$

样例 #1

样例输入 #1

5
7
1 1 1 2 2 4
5
5 5 1 4
2
1
3
3 1
6
1 1 1 1 1

样例输出 #1

4
4
2
3
4

提示

The image depicts the tree from the first test case during each second.

A vertex is black if it is not infected. A vertex is blue if it is infected by injection during the previous second. A vertex is green if it is infected by spreading during the previous second. A vertex is red if it is infected earlier than the previous second.

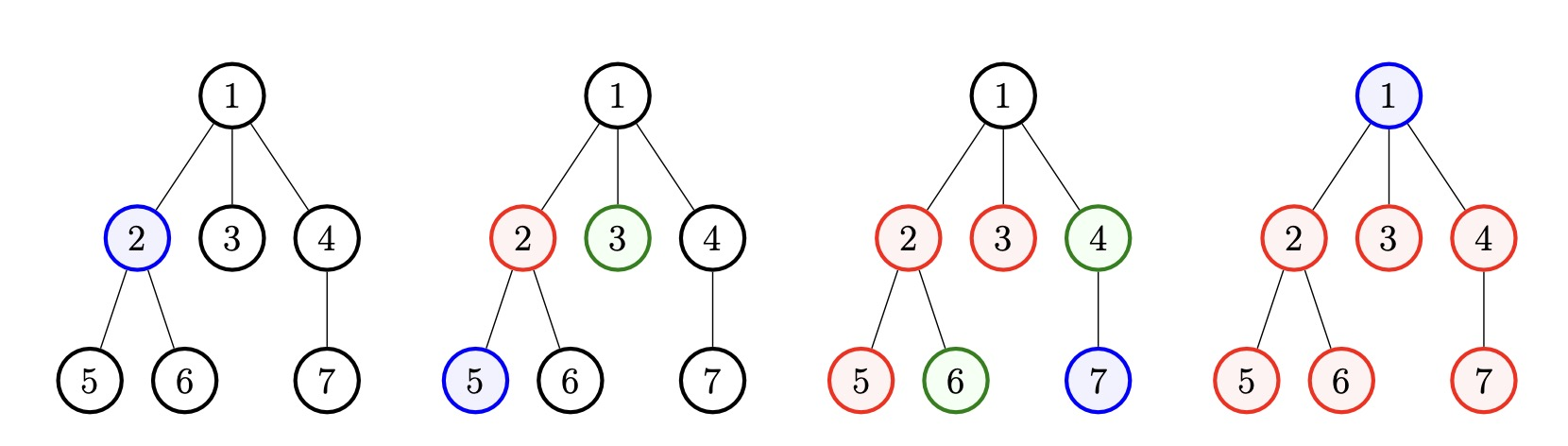Note that you are able to choose which vertices are infected by spreading and by injections.